Unveiling the Essence of Time Series: Components and Decomposition

Time series analysis is an effective method in data science that can be used to find hidden patterns, trends, and anomalies in sequential data. Understanding time series components and decomposition, a complex procedure that breaks down the data into its component pieces and reveals the underlying structure and dynamics, is fundamental to this research. Come along on a journey as we explore the fascinating world of time series components and decomposition, revealing its secrets and realizing its possibilities.


Understanding Time Series Components:





The temporal ordering of time series data, which is the result of sequential observations throughout time, is what makes them unique. It is crucial to understand that time series data is made up of multiple unique components, each of which influences the series' overall behavior while studying the data. These elements consist of:

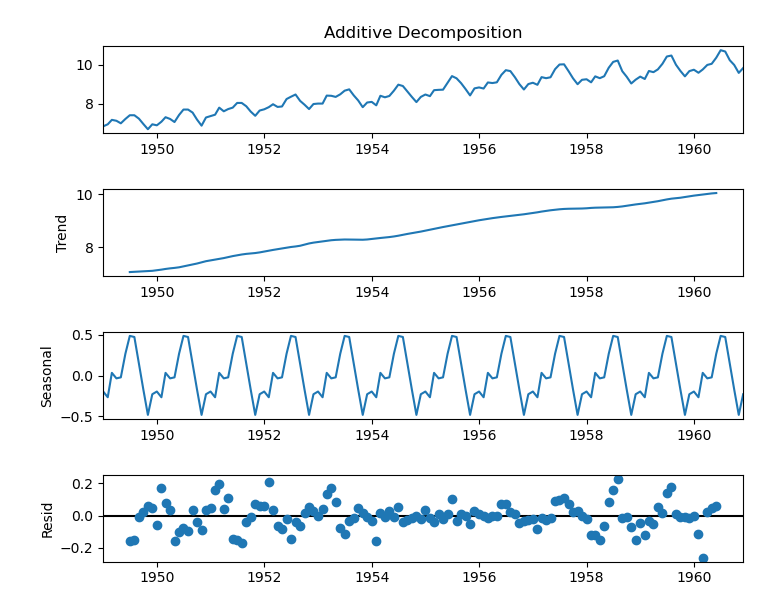
  1. Trend: The long-term movement or directionality seen in the data is represented by the trend component. Trends can indicate general growth, decline, or stability throughout time and can be upward, downward, or stable.
  2. Seasonality: Recurring patterns or changes in data that happen at regular intervals—like daily, weekly, or annual cycles—are referred to as seasonality. Weather, holidays, and economic cycles are just a few examples of the outside influences that frequently affect these patterns.
  3. Cyclic Patterns: Like seasonality, cyclic patterns show periodic changes in the data, but they don't happen at set intervals. Rather, cyclic patterns show longer-duration oscillations or waves, which could last for a few years or even decades.
  4. Irregular or Residual Component: The random or unpredictable fluctuation in the data that cannot be related to a trend, seasonality, or cyclic patterns is represented by the irregular component, sometimes referred to as the residual component. It includes anomalies, random noise, and other unforeseen departures from the underlying pattern.


Decomposition Techniques





By dissecting the time series data into its component parts—trend, seasonality, cyclic patterns, and residual—decomposition enables us to examine each part independently and obtain a better understanding of the underlying dynamics. In time series analysis, a number of decomposition techniques are frequently employed, such as:

  1. Classical Decomposition: Using mathematical methods like moving averages or exponential smoothing, the time series data is divided into its trend, seasonal, and residual components in the classical decomposition method. This technique works well with time series data that exhibit regular, observable patterns.
  2. Seasonal Decomposition of Time Series (STL): Using locally weighted regression smoothing, the STL decomposition method—also called Seasonal and Trend decomposition using Loess—is a flexible and resilient technique that breaks down time series data into trend, seasonal, and residual components. Time series data with non-linear trends and erratic seasonal patterns work well with this technique.
  3. Wavelet Decomposition: With the help of the potent technique of wavelet decomposition, which divides time series data into several frequency bands, we can examine the data at various resolutions. Finding transitory patterns, abrupt changes, and multi-scale dynamics in the data is where this method really shines.

Applications and Implications


Comprehending the components and decomposition of time series holds significant ramifications in a wide range of sectors and fields. Analysts are able to make well-informed decisions, predict future trends, and spot anomalies or outliers by breaking down the data into its component pieces and identifying underlying trends, seasonal patterns, and cyclic fluctuations. The insights obtained from time series decomposition can guide strategic planning, optimize resource allocation, and spur innovation in a variety of fields, including financial forecasting, economic analysis, demand forecasting, and weather prediction.



Conclusion


As we come to the end of our investigation of time series components and decomposition, it is clear that the key to realizing the full potential of time series data is comprehending its underlying structure and dynamics. Analysts can obtain deeper insights into the underlying patterns and linkages by breaking down the data into its trend, seasonality, cyclic patterns, and residual components. This helps them identify anomalies, generate more accurate predictions, and guide decision-making. Let's embrace the richness and complexity of the data as we continue to explore the field of time series analysis, knowing that hidden inside are the secrets to comprehending and influencing the future.


Comments

Post a Comment

Popular posts from this blog

Mastering the Future: An In-Depth Exploration of Advanced Time Series Forecasting Techniques

Image
 Acquiring proficiency in advanced time series forecasting methods is an example in the ever-changing field of data science, enabling analysts to decipher temporal data complexity and reveal future insights. This comprehensive guide explores the complexities of advanced forecasting methodologies, building on readers' core knowledge of time series analysis. It provides readers with the skills and strategies they need to traverse the rapidly changing field of predictive analytics. 1. Autoregressive Integrated Moving Average (ARIMA) Models: The Autoregressive Integrated Moving Average (ARIMA) model, a potent framework for capturing the intricate dynamics of temporal data, is at the forefront of advanced time series forecasting. To model non-stationary time series data, ARIMA models integrate the differencing (I), moving average (MA), and autoregressive (AR) components. Analysts can produce precise and trustworthy forecasts for upcoming observations by using ARIMA models, which help to...
Read more

Unraveling Seasonality: Strategies for Handling Seasonality in Time Series Analysis

Image
Seasonality presents a special problem in time series analysis because it introduces recurrent patterns and variations that can mask underlying trends and skew predictions. For time series analysis to be accurate and trustworthy, seasonality must be understood and managed well. This allows analysts to find important insights and make defensible conclusions. We examine numerous approaches to detecting, quantifying, and reducing seasonality in time series data in this comprehensive reference, giving readers the skills and knowledge they need to competently and confidently negotiate the intricacies of seasonal trends. Understanding Seasonality When recurrent patterns or changes in time series data are seen at regular intervals—like daily, weekly, or annual cycles—they are referred to as seasonality. These patterns can have a big impact on the behavior and dynamics of the data and are frequently influenced by outside variables like the weather, holidays, or economic cycles. Typical illustr...
Read more

Deciphering the Accuracy: A Comprehensive Guide to Model Evaluation in Time Series Analysis

Image
 Choosing the appropriate forecasting model is merely the first step in the field of time series analysis. Ensuring the chosen model is accurate and reliable is essential for guiding strategic planning and helping make well-informed decisions. Analysts can evaluate their forecasting models' performance and verify their prediction powers by using model assessment as a litmus test. We set out to investigate the nuances of model evaluation in time series analysis in this comprehensive guide, giving readers the skills and knowledge they need to confidently and competently traverse the challenging field of predictive analytics. 1. Splitting Time Series Data: It's critical to divide the time series data into training and testing sets before beginning the model evaluation process. The forecasting model is trained using past data from the training set, and its performance is assessed using data from the testing set that has not yet been observed. Typical methods for dividing time serie...
Read more